Completeness Analysis
The completeness of a token sequence describes that all theoretically possible tokens (based on the chosen alphabet and the number of digits) appears in fact in a completed production line. The proof of the completeness of a completed token sequence for short tokens of a given alphabet allows the proof to be generalized for all arbitrarily long tokens of the same alphabet, provided that the same algorithm is used.
The evidence of the completeness of a complete token sequence for short tokens for given alphabets is demonstrated here in a visual, both a qualitative and a quantitative way using patterns found in numerical mappings of token sequences and their analytic transformations.
Qualitative evidence is provided by considering the achievement of defined endpoints of score walks for multiple completed token sequences of the same type.
Quantitative evidence links the successive bits of the individual tokens logically with each other via XOR. Depending on the number of characters in the alphabet, a special parity results in the case of completeness: If the number of characters in the alphabet is even, then the maximum possible number of tokens in a sequence is even and the bitwise parity is zero. If the number of characters in the alphabet is odd, the maximum possible number of tokens in a sequence is odd and the character-wise parity is the XOR of all characters in the alphabet.
Analysis Archives
DICE - Completeness Analysis Archive (9.0 MB)
FIVE - Completeness Analysis Archive (5.2 MB)
FRUITS - Completeness Analysis Archive (9.4 MB)
SWEET - Completeness Analysis Archive (5.3 MB)
The linked archives contain
- some metrics of the tokens, of the scores and of the deltas as JSON
- the token data, the score and delta numbers as CSV
- the score walk numbers and the token check bit counters as CSV
- all available plots as shown below as an example in PNG format
Analysis Plots
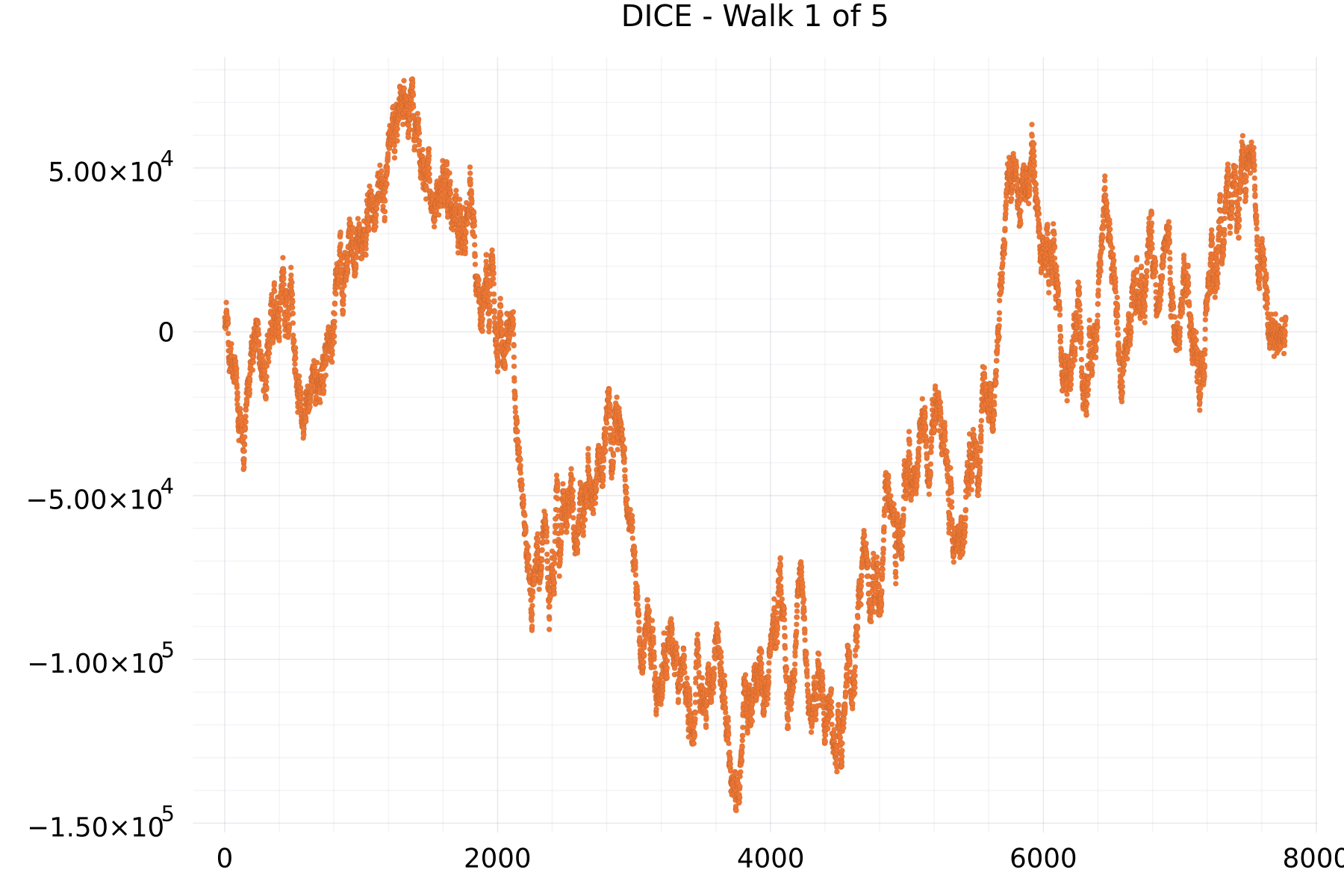
The aim of the completeness plots is to show on qualitative way that the centered score walk patterns of many completed token sequences (5 here to be specific) of the same kind, obtained via the Unique Tokens API, all ends at the same point and are clearly different from each other.
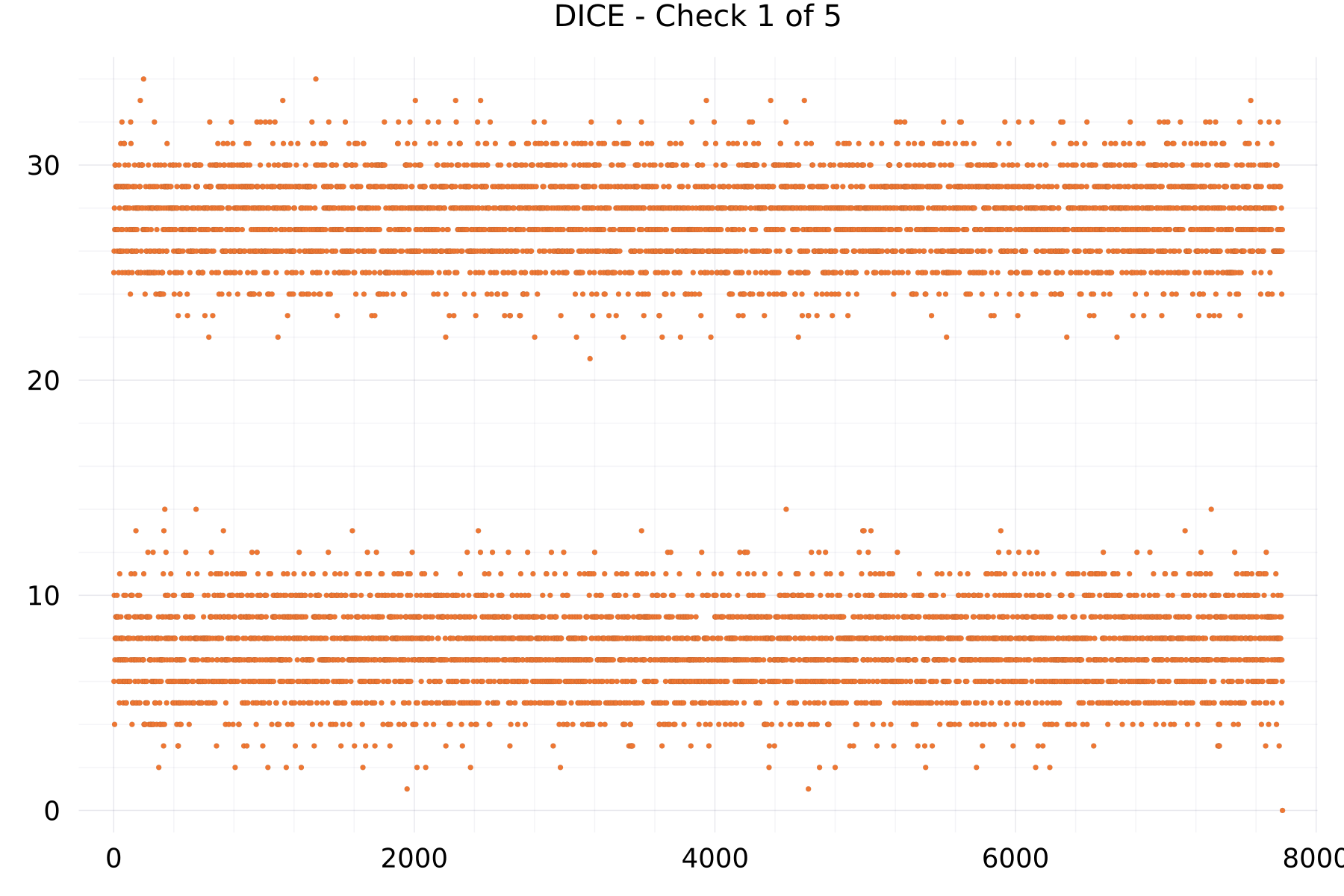
In addition, the accumulated counters of the XOR-ed token bits are shown as an other way to analyze the completeness of short token sequences on quantitative way for any two ASCII and Unicode alphabets with zero- and non-zero parity.
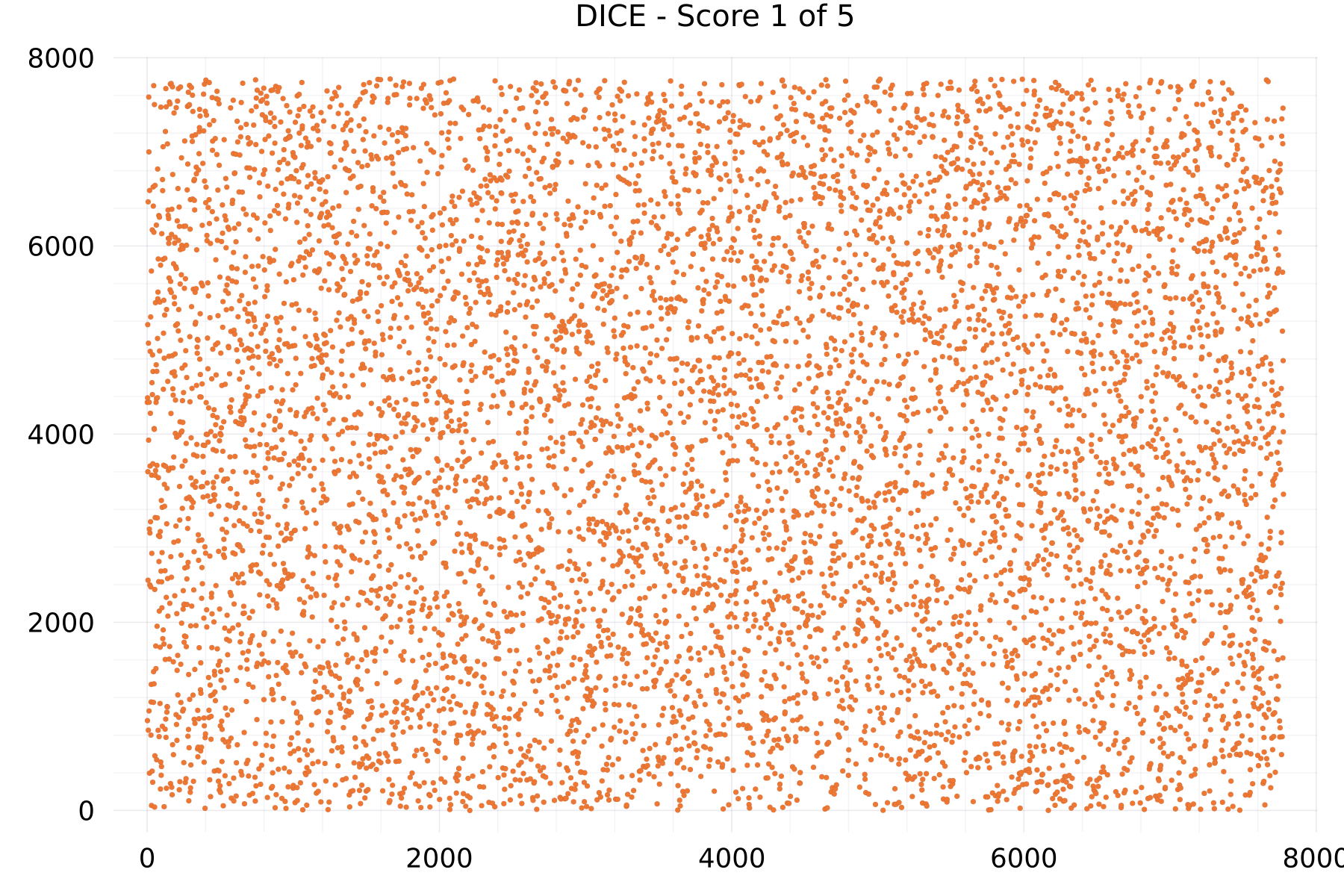
Score Plots
The plot shows as example for the DICE alphabet the numeric scores of many sequences of 7,776 DICE scores.
Walk Plots
The plot shows as example for the DICE alphabet the centered walk of many sequences of 7,776 DICE scores.
Check Plots
The plot shows as example for the DICE alphabet the XOR-ed bits count of many sequences of 7,776 DICE tokens.