Probability Success

Randomized serial numbers (also called tokens) can generally be generated in a purely random, purely deterministic or in a hybrid way and have to meet some technical and regulatory requirements. For example, to meet EPCG Pharma Track & Trace requirements, the production of true randomly generated unique sequences, each consisting of e.g. 1 million 20-digit tokens for the UPPER_EPCG30 alphabet of 30 characters, requires at least a powerful True Random Number Generator (TRNG) and a high-performance database throughout the production process.

Due to the non-deterministic functional principle, the TRNG would ensure the real uniqueness of the many sequences. For each new token, 20 characters are randomly, equally distributed and independently drawn from the 30 characters of the alphabet and assembled into a new token. This token would then be searched for in the sequence to be created in the database and only added there if it was not already there.

This hypothetical technical procedure raises (for mathematicians) an interesting question: How long is a sequence of new tokens after this algorithmic task has run 1 million times? As a reminder, this is the number of tokens required for each new unique sequence in our example. The answer is, it depends, as it is a probabilistic phenomenon and can therefore only be answered in probabilities over a large number of trials!

It can be proven that, over a large number of trials, the probability of finding a new token with n possible tokens after n attempts converges asymptotically to the lower limit 1 - ℯ⁻¹ ≈ 0.6321. The symbol ℯ stands for Euler's number. That means, that each procedure to build a new token sequence can also require significantly more than just n attempts.

In contrast, the Unique Tokens API is based on a highly optimized, hybrid algorithmic design that uses a deterministic, high-dimensional cellular automaton that is differently constructed and initialized for each new production line by a TRNG. This ensures on the one hand that no database is required and linear time complexity applies, and on the other hand that each new production line forms a truely different token sequence with perfect randomness.

To illustrate the runtime-consequences (solely due to the operating principle of the algorithm, the database-related expenses are not yet taken into account here) of this fundamental difference, the probability of finding a character over the number of tries for an alphabet of 30 characters is shown below using a deterministic versus randomized approach:

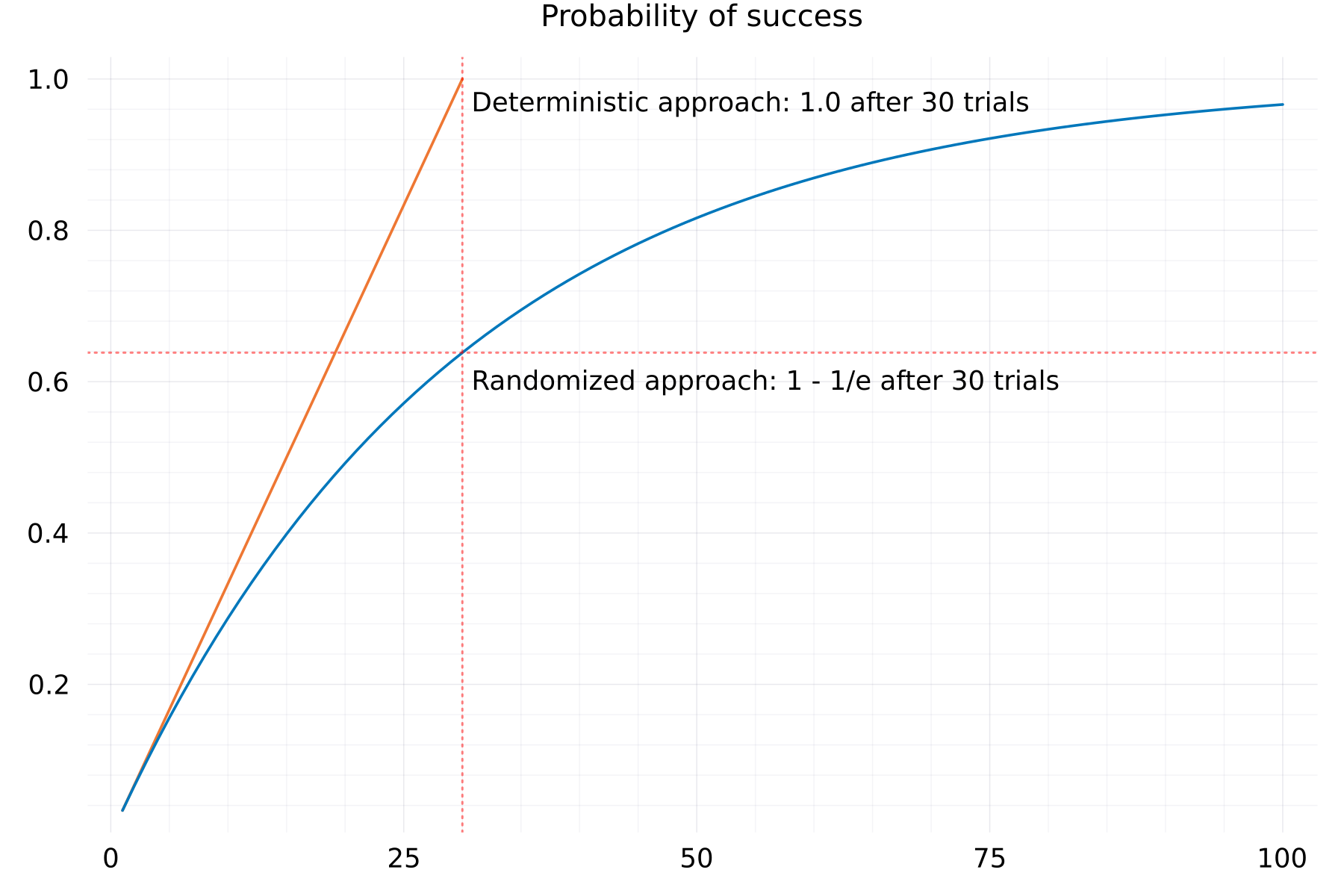
If tokens can also be generated by a hybrid algorithmic design instead of in a purely random way (using a TRNG and a database), the question of an explorative and comparative data analysis arises. On the following pages some probabilistic properties and meta-properties of real token sequences, obtained via the Unique Tokens API, are presented.