Uniqueness Analysis
The uniqueness of many token sequences of the same kind describes that each new production line builds a distinctly different token sequence, especially without (non-trivial) common analytical properties or similar stochastic patterns. Every token sequence is neither reproducible nor predictable and there are no identical or similar token sequences, neither in whole nor in part.
The uniqueness of many token sequences of the same kind for given alphabets is demonstrated here in a visual way using patterns found in numerical mappings of token sequences and their analytic transformations.
Analysis Archives
DICE - Uniqueness Analysis Archive (19.9 MB)
UPPER_EPCG30 - Uniqueness Analysis Archive (21.6 MB)
The linked archives contain
- some metrics of the tokens, of the scores and of the deltas as JSON
- the token data, the score and delta numbers as CSV
- all available plots as shown below as an example in PNG format
Analysis Plots
The aim of the uniqueness plots is to show that the patterns found in numerical mappings of many token sequences (5 here to be specific) of the same kind, obtained via the Unique Tokens API, are clearly different from each other.
Some plots show multiple applications of different analysis algorithms, whereby for the moving average a very wide window was chosen with the aim of making the differences easily recognizable visually.
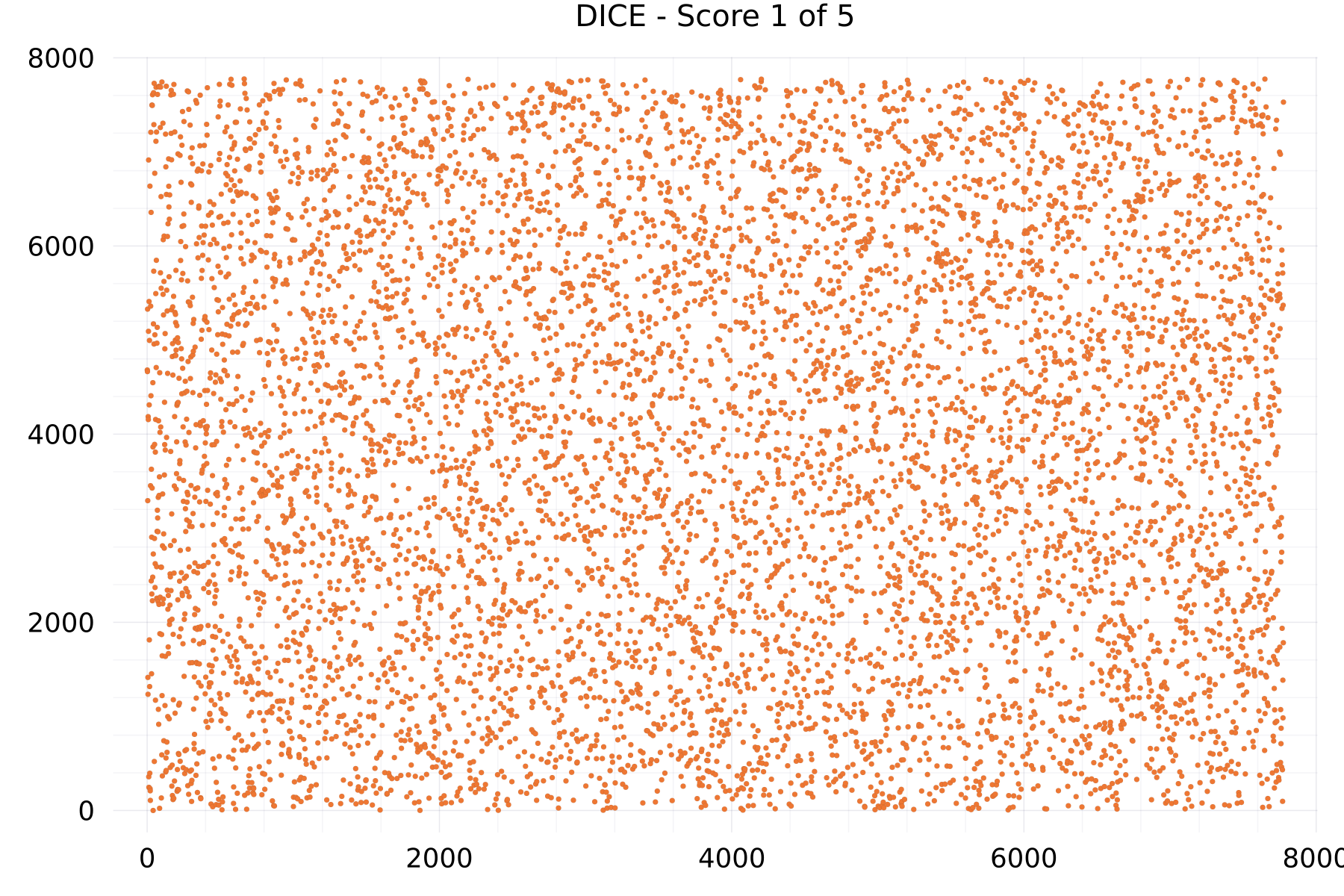
Score Plots
The plot shows as example for the DICE alphabet the numeric scores of many sequences of 7,776 DICE scores.
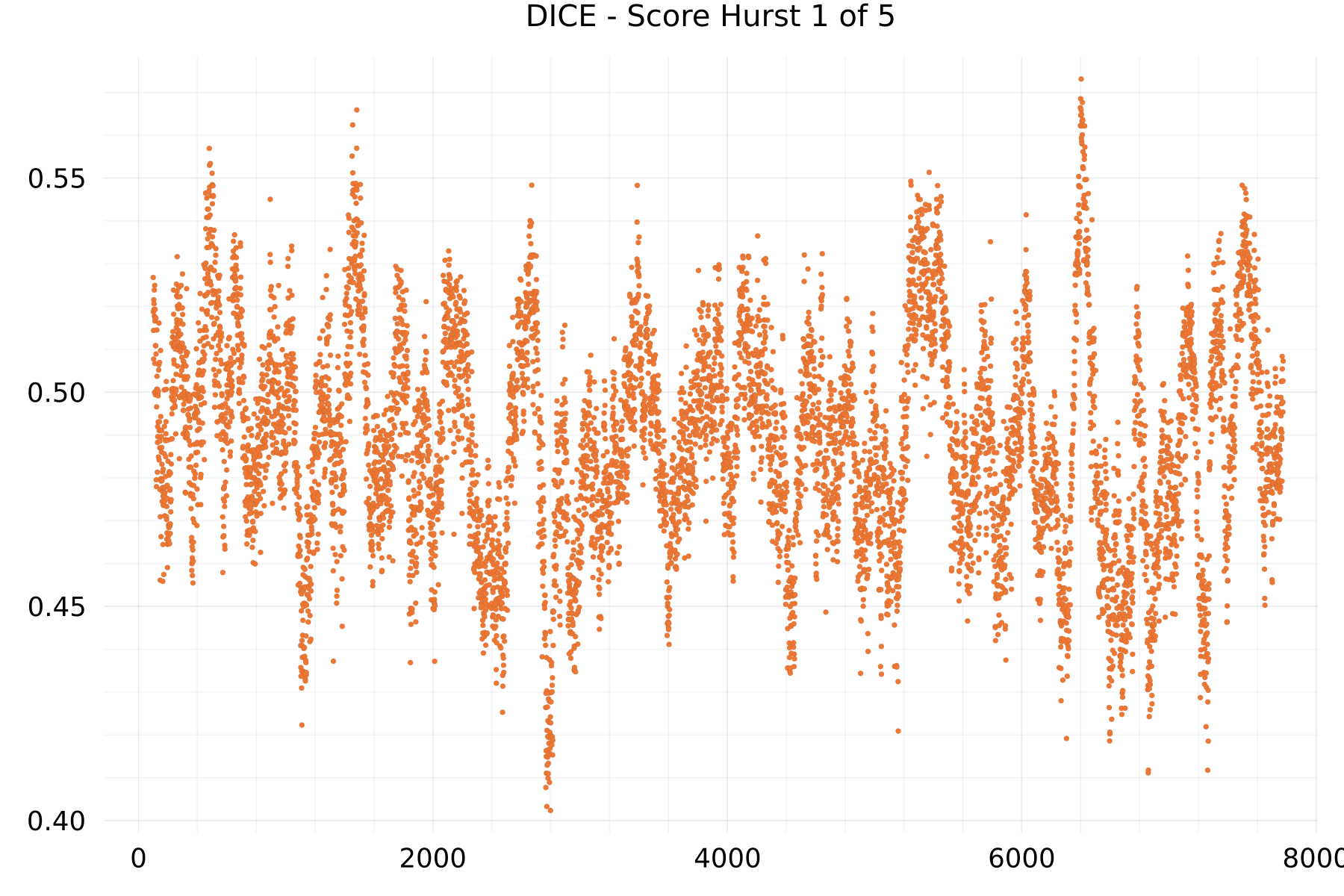
Score Hurst Plots
The plot shows as example for the DICE alphabet the hurst exponent of many sequences of 7,776 DICE scores.
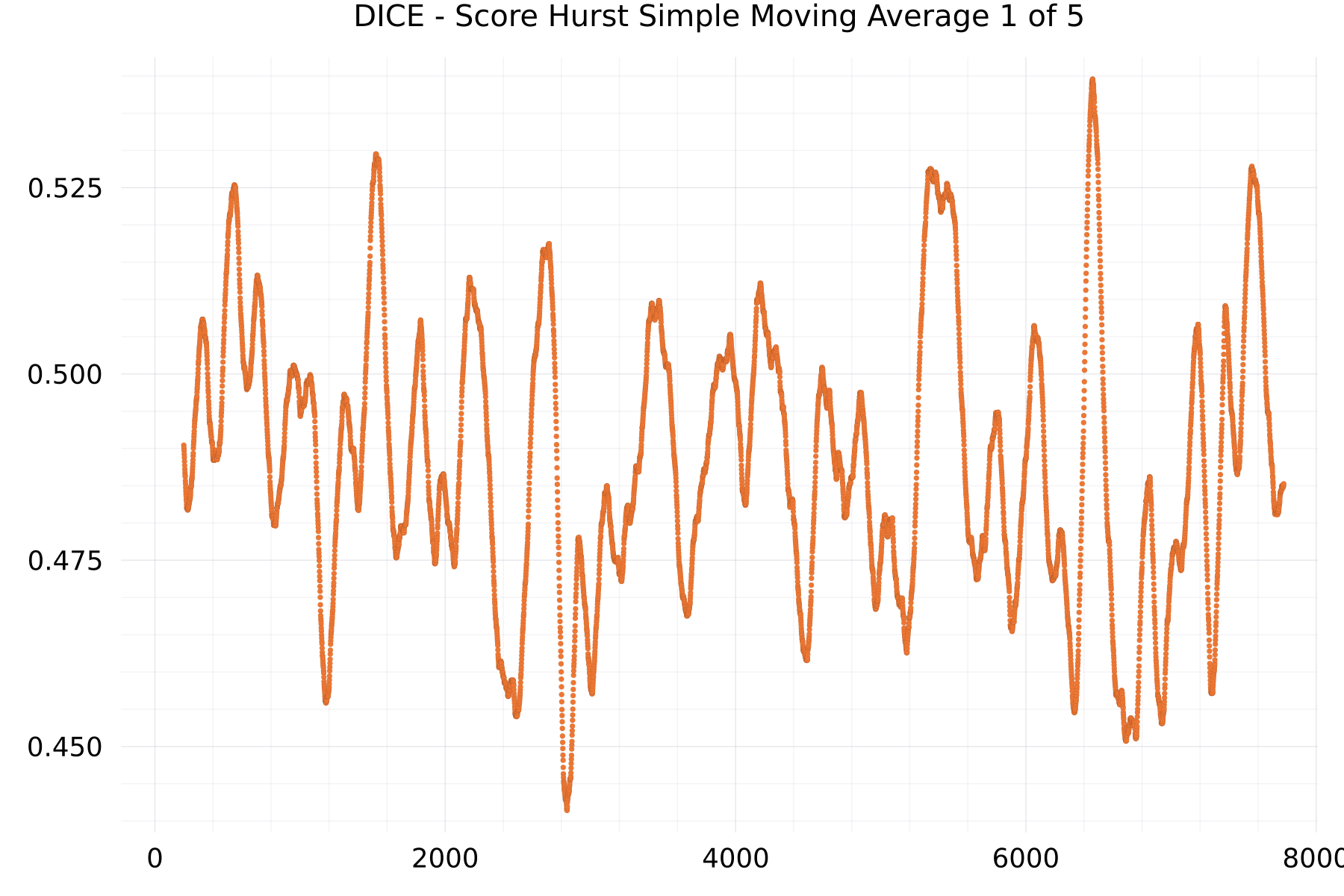
Score Hurst Simple Moving Average Plots
The plot shows as example for the DICE alphabet the simple moving average of the hurst exponent of many sequences of 7,776 DICE scores.
Delta Plots
The plot shows as example for the DICE alphabet the one-step differences of many sequences of 7,776 DICE scores.
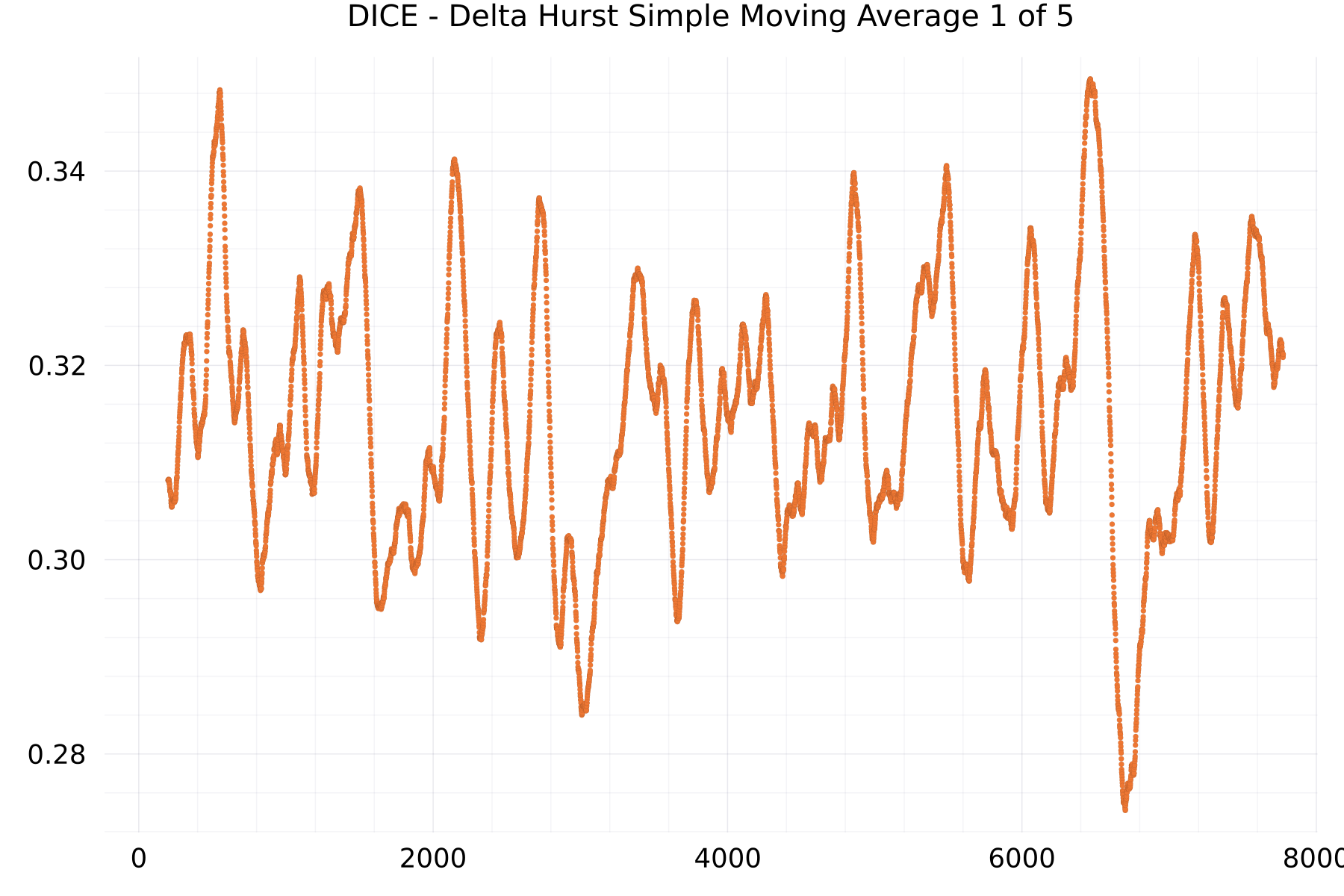
Delta Hurst Plots
The plot shows as example for the DICE alphabet the hurst exponent of many sequences of 7,775 DICE deltas.
Delta Hurst Simple Moving Average Plots
The plot shows as example for the DICE alphabet the simple moving average of the hurst exponent of many sequences of 7,775 DICE deltas.